기술과 솔루션
내후성과 가상공학 II. 내후성 시험과 CAE 해석
작성자 : 편집부
2022-10-13 |
조회 : 6347

I. 서론
부품의 지속적 사용과 재사용에 중점을 둔 제로 웨이스트(Zero waste) 방식인 순환 경제(Circular economy) 개념이 부품 설계에 중요한 전략이 되고 있다. 본 연재의 배경은 제품수명연장(Product life extension)을 통한 순환 경제 구현의 새로운 솔루션 제공에 있다.
제품수명연장은 사용될 제품의 이용률 및 지속시간을 최대화하도록 설계하는 것에서 출발한다. 제품을 버릴 때마다 제품 생산에 투입된 에너지와 자원 역시 함께 소멸된다.
제품 폐기로 인해 소멸되는 자원을 순환시킬 목적으로 재사용 및 재활용이 고려되는데 제품수명연장은 폐기물 수거 이후 분리나 재사용 또는 재활용에 소모되는 에너지와 자원을 미리 줄일 수 있다는 점에서 효과적인 선제적 친환경 솔루션이라 볼 수 있다.
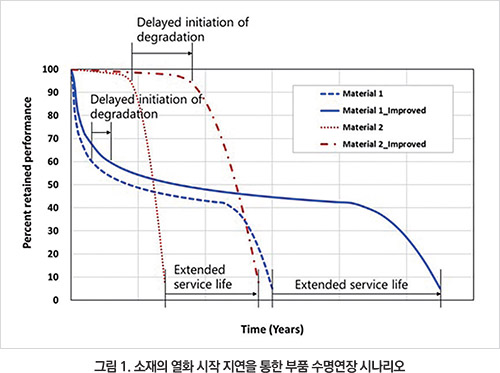
부품의 장기 사용관점에서 내후 성능 평가 및 수명 예측이 중요한 설계 과정이며, 이에 대한 평가 및 설계 방법론을 제시한다. 내후 노출 부품에 대한 수명연장 설계의 이점은 그림 1에 보여지는 바와 같이 내후 열화에 의한 물성 저하 시점을 지연시킴으로 부품의 사용 수명을 연장할 수 있다는 것이다.
이전 9월호에 게재된 원고에서는 그동안 플라스틱 소재의 내후성 시험에서 언급되지 않았던 4가지 인자(내후 시편의 거치 조건, 시편의 두께, 시편 제조방식에서 발생할 수 있는 잔류응력, 그리고 내후 수명 모델 개발을 고려한 내후 시험 시간)을 제시하였고, 내후 시험 시간을 제외한 나머지 3가지 인자에 대한 영향도를 설명하였다.
본 보고서는 지난 보고서에서 설명하지 못한 내후 시험 시간 설정의 중요성에 대한 설명을 먼저 마무리한 후 4년의 자연광 노출 시험 사례 중심으로 기계적 물성의 열화 거동 분석, 수명 예측 모델 개발, 그리고 내후 CAE 해석을 위한 절차 및 가상 사례를 통한 내후 CAE 해석의 효용에 대하여 설명한다. 참고로 본 보고서에 실린 많은 내용은 참고문헌1을 간략하게 재구성한 것이다.
1.1 설계 관점에서 고려할 내후성 시험 인자 - 내후 시험 시간
내후 시험 시간은 시험의 경제성과 사용 수명 예측(Service Life Prediction, SLP) 모델의 신뢰성 확보에 큰 영향을 주는 변수이다. 신속한 부품개발과 비용 절감을 위해서 촉진 내후 시험(Accelerated weathering tests)이 흔히 사용된다.2
촉진 내후 시험은 그림 2에 보여지는 바와 같이 설정된 목표 물성값이 실제 자연환경에 장기간 노출되면서 발생하는 물성 저하 추세를 잘 대변할 수 있어야 촉진시험으로써 효용가치가 있다.3-4 촉진시험과 자연광 시험의 결과로부터 충분한 연관성이 확인되면 식 (1)과 같이 등가 시간(Equivalent time) 또는 가속 계수(Acceleration factor, k)를 제시할 수 있다.
예를 들면, 지역별 편차는 있지만 300~400㎚ 자연광 파장에 대한 1년 누적 광량을 250MJ/㎡으로 추정한다.
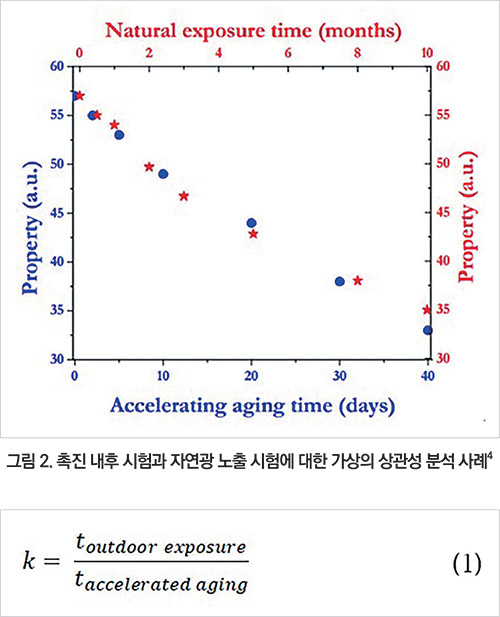
자동차 외장재에 대한 실내 촉진시험으로 널리 알려진 SAE J2527 기준(340㎚ 파장 기준, 0.55W/㎡)5으로 1년의 자연광 노출에 따른 플라스틱 외장품의 열화 거동 시험을 진행한다면 내후 시험 기간은 약 79일이 소요된다. 1년의 누적 광량의 촉진시험이지만, 자동차 운행 시간과 주차 장소를 고려하여 누적 광량 250MJ/㎡을 2년의 실제 운용 시간으로 추정하는 것이 일반적이다.
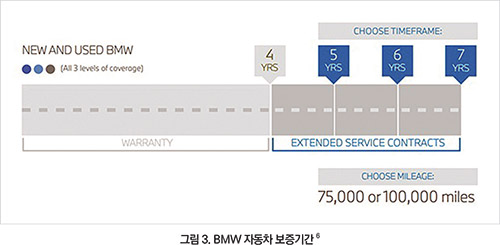
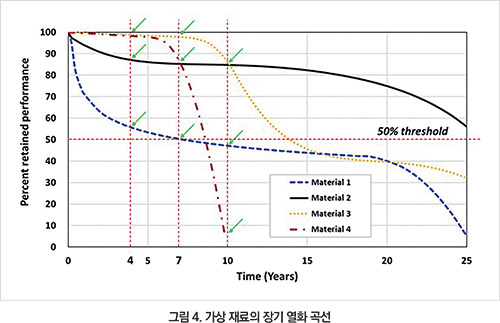
만약 그림 3에 보여지는 것처럼 자동차 회사가 일반 보증(4년/5만 마일)과 연장 보증(7년/10만 마일)을 제시했다면, 그림 4와 같은 후보 소재가 검토될 때, 시험 시간에 따라 상이한 소재를 선정하게 된다.
4년 보증(소재 4와 3 > 소재 2 > 소재 1), 7년 보증(소재 3 > 소재 4와 2 > 소재 1) 또는 10년 보증(소재 3과 2 > 소재 1 > 소재 4)에 따라 소재의 선정이 달라질 것이다. 이처럼 내후 시험 시간에 따라 내후 성능에 대한 판단기준이 달라질 수 있으므로 부품의 보증기간을 고려하여 내후 시험 기간을 주의 깊게 결정해야 한다.
주의할 점은 내후 시험에서 물성 열화를 ‘내후 시험 시간’ 경과에 따른 변화라고 설명하였지만, 엄밀히 말하면 내후 시험 기간 동안 소재나 부품이 받게 되는 ‘누적 광량(Cumulative UV dose or UV radiation)’에 따른 물성 열화라는 점이다.
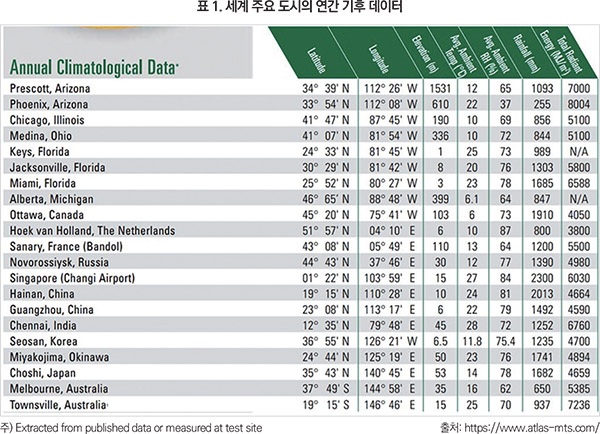
자연광은 표 1에 보여지는 바와 같이 지역별로 다르므로 내후 시험 결과를 비교할 때는 물리적 시간에 대한 비교가 아닌 시험 조건별 동일 누적 광량에 대해 결과 값을 비교해야 한다.3
Ⅱ. 플라스틱 소재의 내후성 시험
2.1. 고분자 소재 및 4년 자연광 노출 시험
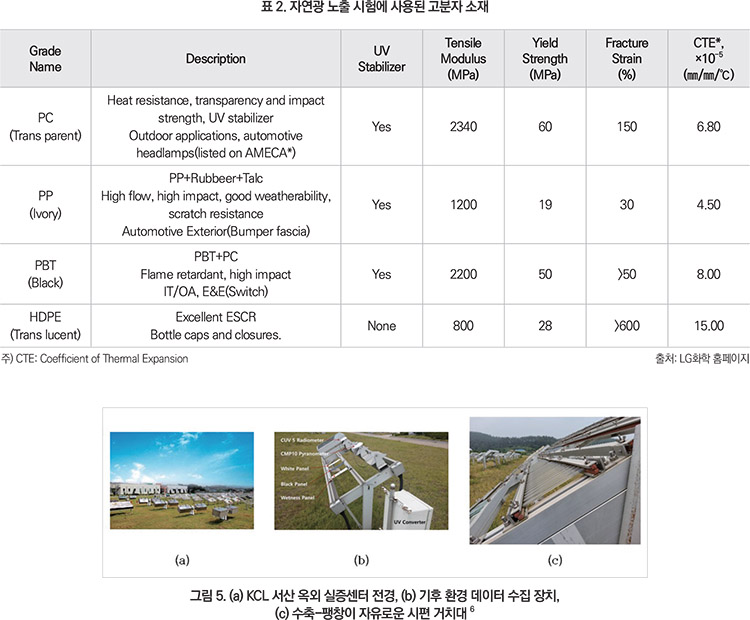
표 2에 정리된 바와 같이 내후 노출을 받는 대표적인 4가지 적용 분야와 소재를 선정하고, 4년의 자연광 노출 시험을 진행하였다. 4년 동안 315~400㎚ UV 파장대에서 누적 광량이 60MJ/㎡에 도달했을 때마다 주기적으로 인장 시편을 수거하여 물성을 측정하는 방식으로 총 1,020MJ/㎡까지 시험을 진행하였다.
내후 시험은 그림 5와 같이 한국건설생활환경시험연구원(KCL, www.kcl.re.kr)의 옥외 실증센터가 위치한 서산에서 진행하였고, 열 피로에 의한 시험 결과의 편차를 최소화하기 위해 그림 5c에 보여지는 바와 같이 온도변화에 대해 자유롭게 수축-팽창할 수 있는 거치대를 고안하여 활용하였다(특허 등록번호: KR1021150250000).
2.2. 4년 자연광 노출 시험 결과
2.2.1. 4년 기후 정보
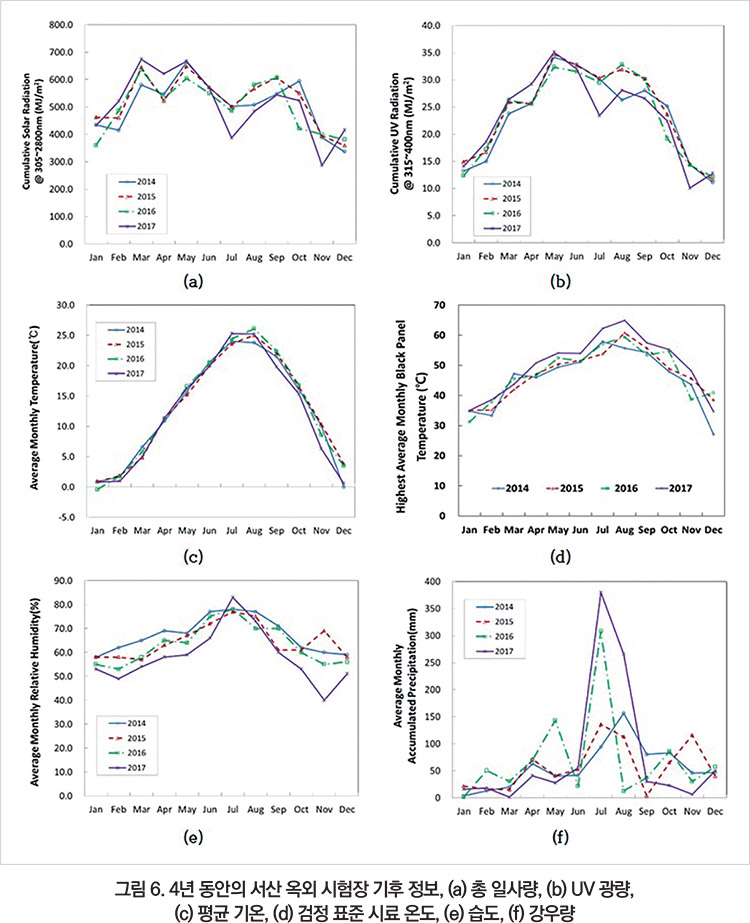
4년간의 서산 옥외 시험장의 월별 평균 기후 정보를 정리하면, 그림 6과 같다. 내후 시험에서는 총 광량보다 UV 파장대가 중요하며, 5월에 UV 광량이 가장 많음을 알 수 있다(그림 6b).
315~ 400㎚ 영역에서 연간 누적 UV 광량은 283.5MJ/㎡였다. 기온 변화에 따른 열 피로 응력이 염려된다면 기온 변화보다는 검정색 표준 시료(BPT, Black Panel Temperature)의 온도변화를 참조하는 것이 더 바람직하다(그림 6d).
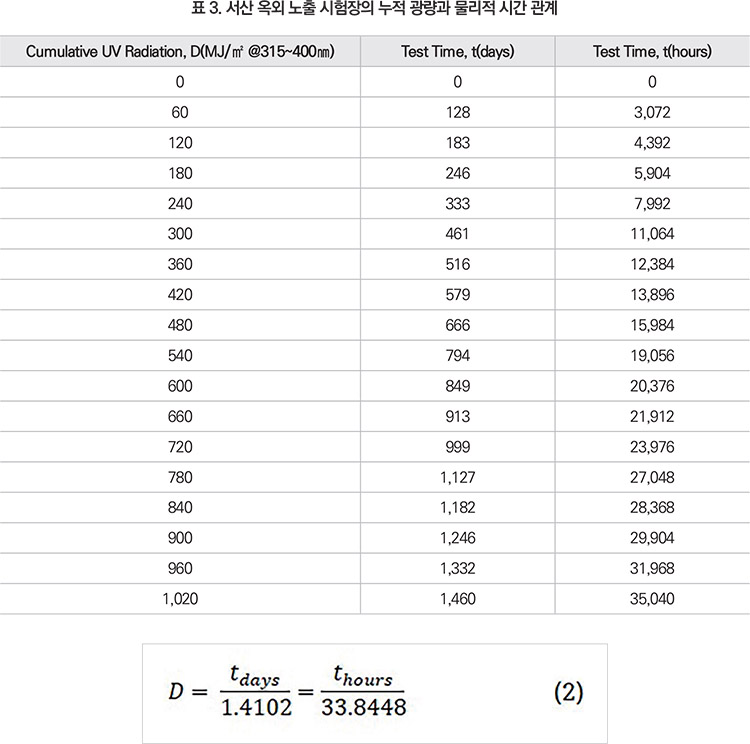
앞 절에 설명한 바와 같이 소재의 내후 열화는 내후 시험 시간에 비례하기보다 누적 광량에 비례하며, 내후 시험 시간(t)과 누적 광량(Cumulative UV dose, D)의 관계식을 파악해두는 것은 내후 수명 예측에 있어 중요하다.
그림 6a와 6b에서 알 수 있듯이 광량은 월별로 다르다. 서산 지역의 60MJ/㎡ 광량 주기에 대한 물리적 시간은 표 3과 같으며, 이를 바탕으로 상호 연관성을 파악하면 식 (2)와 같다.
2.2.2. 4년 자연광 노출 시험 결과
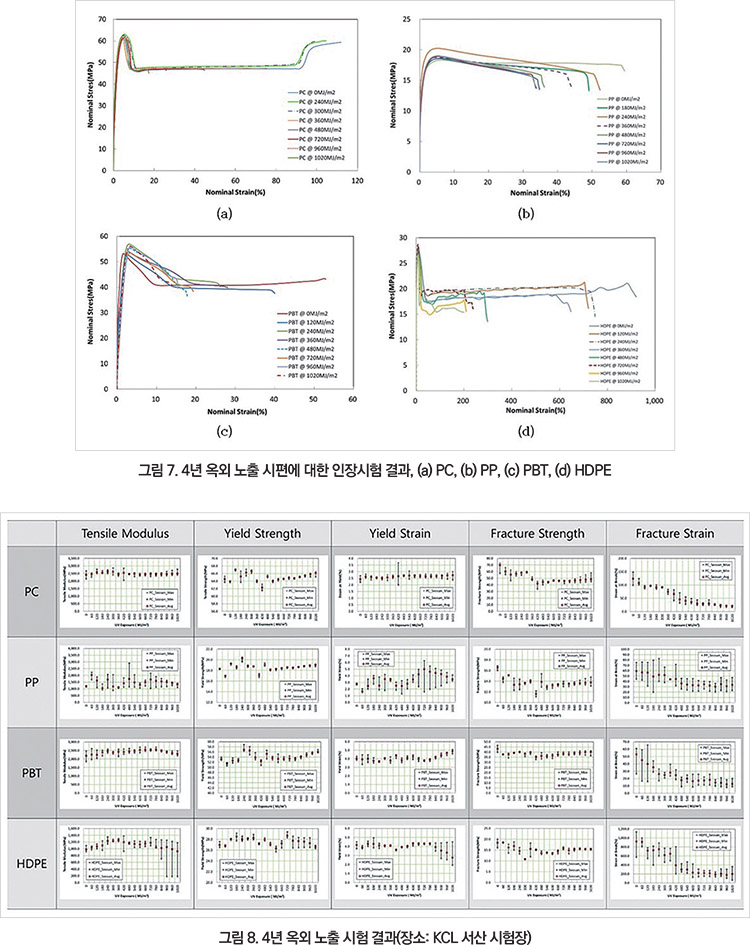
4년 동안 60MJ/㎡ 광량 주기로 측정한 4종 고분자 소재의 인장시험 결과는 그림 7과 같다. 인장시험 결과로부터 탄성계수, 항복강도, 항복신율, 파단강도, 파단신율을 추출하여 정리하면 그림 8와 같다.
2.3. 내후 열화 거동 예측 모델
그림 8에 정리된 4종 소재의 기계적 물성 거동을 살펴보면, 소재의 탄성 거동을 설명하는 물성(탄성계수, 항복강도, 항복신율)은 4년 동안 초기 값이 거의 유지되는 반면, 소성 거동을 설명하는 물성(파단강도와 파단신율)은 저하되는 경향성을 보인다.
특히 파단신율의 저하가 가장 두드러지게 관찰된다. 각 영역별 열화 거동 특성을 고려하여 다음과 같은 두 가지 열화 거동 모델을 제안한다.
2.3.1. 탄성 영역 열화 거동 예측 모델 – 지수 성장-감소 모델
소재의 탄성 영역 거동을 설명하는 기계적 물성은 탄성계수, 항복강도, 항복신율이 대표적이다. 4종 소재 모두 4년의 자연광 노출 시험 기간에 초기의 항복신율보다 낮은 영역에서 파단이 발생하는 취성파단을 보이지는 않았으며, 탄성 거동을 대변하는 물성에서도 큰 변화는 없었다.
4년 동안 주기적으로 측정된 이들 세 가지 물성 변화를 살펴보면, 일정 시간 동안 초기 값보다 다소 상승하다가 이후 감소하면서 양의 값에 수렴하는 경향성을 보였다.
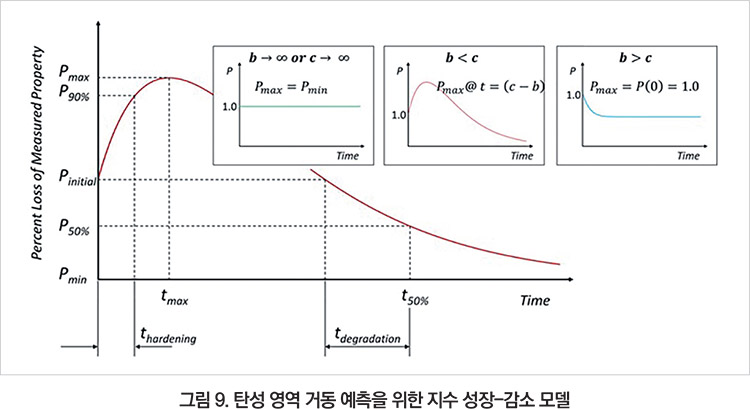
이를 토대로 식 (3)에 보여지는 바와 같은 초기에 성장했다가 일정한 양의 값으로 수렴하는 ‘지수 성장-감소 모델(Exponential growth and decay model)’을 도출하였다. 물성 항목별 측정값 변화를 균일화하기 위해 초기 값(Vinitial) 대비 측정 시점의 물성(Vcurrent)을 비교하는 물성 유지율(P= Vcurrent⁄Vinitial) 개념을 도입하였다. 그러므로 초기 시간에서의 물성 유지율은 1.0에서 시작한다.
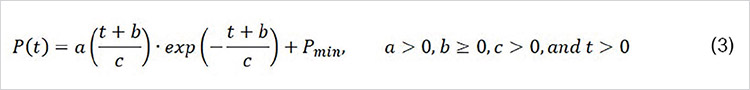
여기서 t는 식 (2)에 보여지는 바와 같이 내후 노출 지역별 광량에 따라 누적 광량(D)으로 치환될 수 있으며, a, b, c 및 Pmin은 물질 상수이다. 각 물질 상수의 조건에 따라 탄성 영역 거동은 그림 9에 보여지는 바와 같이 다르게 예측될 수 있다.
2.3.2. 소성 영역 열화 거동 예측 모델 – 역 로지스틱 모델
소재의 소성 영역 거동을 설명하는 기계적 물성은 파단강도와 파단신율이 있다. 인장시험에서 파단점은 시편이 완전히 분리되는 지점이다.
파단강도는 파단점에서의 응력 값이다. 일반적으로 연성 재료는 항복강도(엄밀히 말하면 극한 인장강도, UTS, Ultimate tensile strength)보다 낮은 파단강도를 갖는 반면, 취성 재료는 극한 항복강도와 동일하다.
그러나 플라스틱 소재의 경우, 파단 시점이 명확하지 않은 경우가 있어 파단 응력이 다양하게 측정될 수 있음에 주의해야 한다. 그러므로 내후 노출에 의한 플라스틱 부품의 열화 정도를 판단하는 기준으로 파단강도보다는 파단신율이 합리적이다.
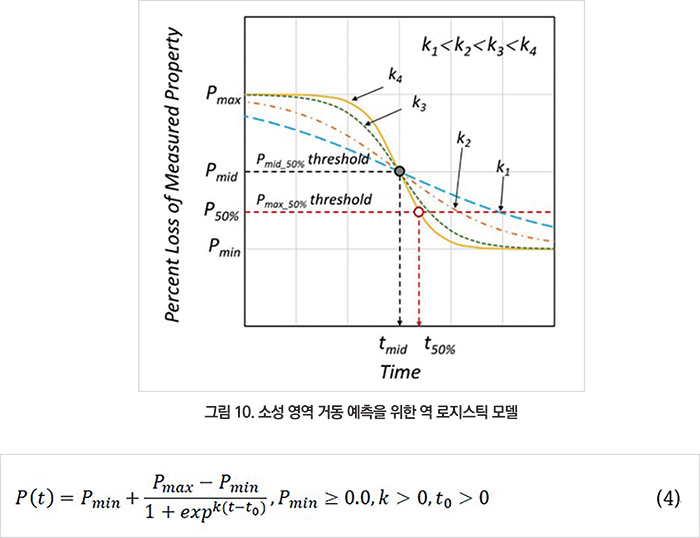
4년 동안 주기적으로 측정된 파단강도와 파단신율의 변화를 살펴보면, 일정 기간동안 초기 값을 유지하다가 감소한 이후 임의 값으로 수렴하는 경향성을 보였다. 이를 토대로 그림 10과 식 (4)에 보여지는 바와 같은 초기 값이 일정 기간 유지되다가 감소한 이후 임의 값으로 수렴하는 ‘역(逆) 로지스틱 모델(Inverted logistic regression model)’을 도출하였다.
여기서 t, Pmin, Pmax는 각각 시간, 최소 및 최대 유지 값이다. k는 로지스틱 성장률 또는 로지스틱 곡선의 기울기, t0는 역 로지스틱 곡선의 중간점(tmid)이다. 0.00.5일 때 Pmin은 풍화 노출로 인해 특성이 더 이상 감소하지 않는 내구 한계 값이다.
2.4. 내후 열화 거동 예측 결과
4년 자연광 노출 시험에 대한 60MJ/㎡의 광량 주기로 인장시험을 진행하였음으로 누적 광량(D) 기준으로 예측하였다. 탄성 영역 거동은 식 (5)로 예측하며, 소성 영역 거동은 식 (6)으로 예측한다.
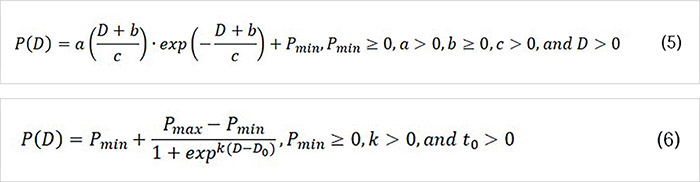
1.1절에 설명한 바와 같아 내후 시험 시간은 장기 내후 수명 예측에 있어 중요한 변수가 된다. 본 연구에서는 2년 노출 결과를 토대로 한 수명 예측 모델과 4년 노출 결과를 토대로 한 수명 예측 모델을 비교해 보았다. 4종 소재 중 PC 소재에 대한 장기 내후 거동 예측 결과는 그림 11과 같다.
그림 11에 보여지는 바와 같이 2년의 노출 시험 결과를 토대로 한 거동 예측과 4년의 노출 시험 결과를 활용한 거동 예측이 상이한 것을 알 수 있다. 당연한 결과로 4년의 시험 결과를 활용한 거동 예측 모델이 물성 열화 거동을 더 잘 따르고 있다.
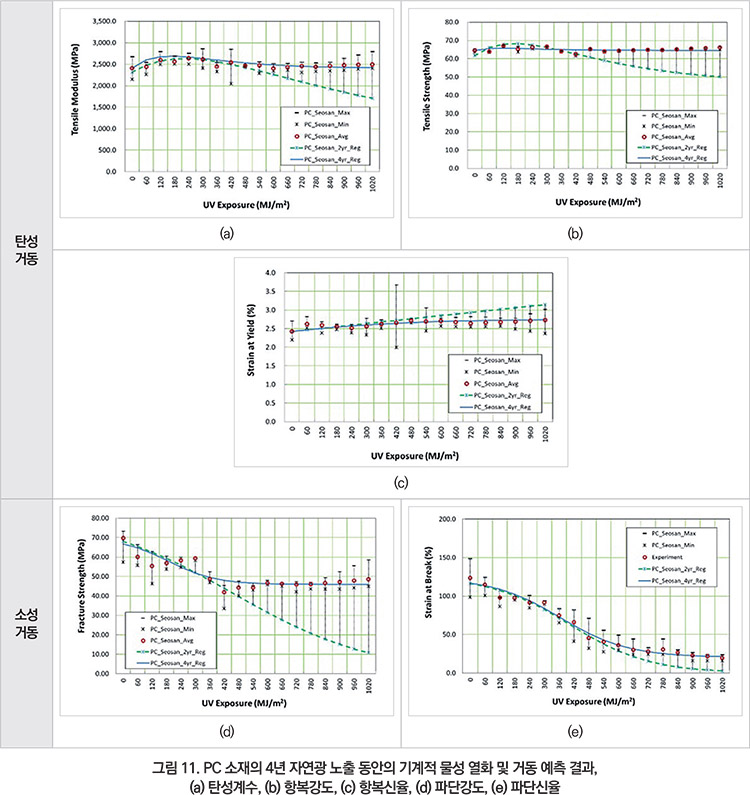
소재별 회귀분석 변수를 적용하여 물성 유지율을 계산한 다음 초기 값을 곱하여 열화 물성을 추정할 수 있다. 장기 내후 노출 플라스틱 파손 여부는 파단신율의 열화에 의해 결정되는 경우가 많다.
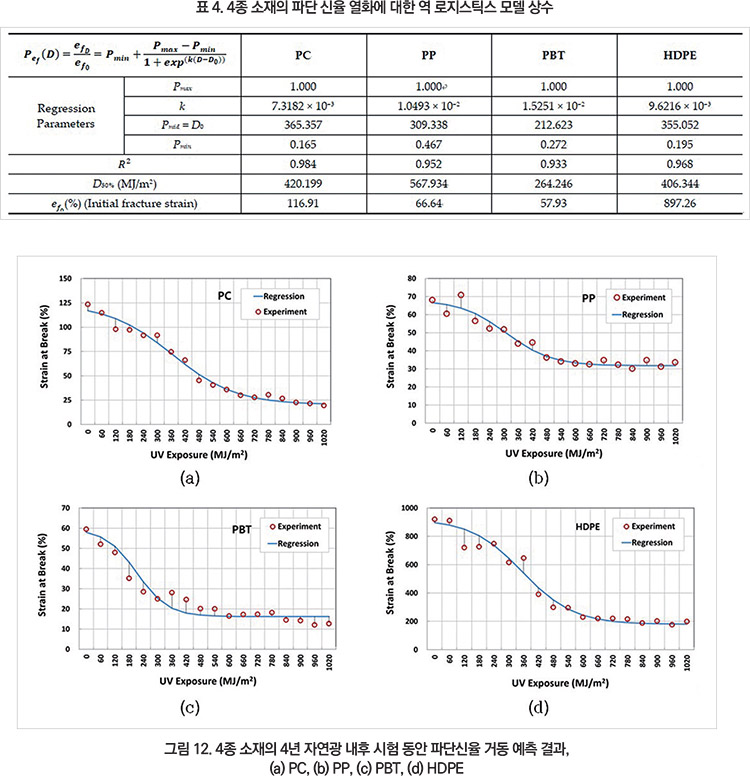
7-11 4년 노출에 의한 파단신율의 열화 거동을 역 로지스틱 모델로 예측해보면, 표 4와 그림 12와 같다. 표 4에 보여지는 바와 같이 예측 모델의 적합도를 나타내는 결정계수(Coefficient of Determination, )는 0.9 이상으로 매우 높았다.
Ⅲ. 내후 CAE 해석
내후 노출 플라스틱 부품에 대한 유한요소해석(Finite Element Analysis, FEA)을 진행하기 위해서는 공칭 응력-변형률(Nominal Stress-Strain) 곡선으로부터 외력에 의한 시편의 단면적 변화가 고려된 진응력-진변형률(True Stress-Strain) 곡선을 구해야 한다.
유한요소해석을 위한 물성 거동 모델링에 있어 가장 먼저 정의해야 하는 것이 플라스틱 소재의 가역적인 탄성 거동과 비가역적인 소성 거동으로 구분하는 것이며, 이를 구분하는 기준점이 항복신율이 된다. 항복신율은 탄성계수와 항복강도에 의해 결정되므로, 진응력-진변형률 계산에 있어 탄성계수와 항복강도의 결정이 중요한 변수가 된다.
3.1. 내후 열화를 고려한 유한요소 해석용 진응력-진변형률 계산
유한요소해석의 시작은 해석에 사용되는 소재의 비선형 거동을 대변하는 물성 모델링에서 시작된다. 그림 13a에 보여지듯 고분자 소재는 소재별 처방에 따라 다양한 응력-변형 거동을 보인다.12
일반적으로 고분자 소재를 점탄성 소재(Viscoelastic materials)라 하며, 이를 설명하기 위해 스프링-댐퍼 특성을 활용한다. 그중 대변형을 가지는 고분자 소재에 대한 거동 예측 모델의 대표적인 사례가 그림 13b에 보여지는 Haward와 Thackray 모델이다.13 탄성 영역과 소성 영역의 거동을 정의하는 방식에 따라 다양한 진응력-진변형률 곡선이 도출되므로 주의 깊게 접근해야 한다. 고분자 소재의 탄-소성 거동 예측에 대한 다양한 모델이 제시되었다.13-16
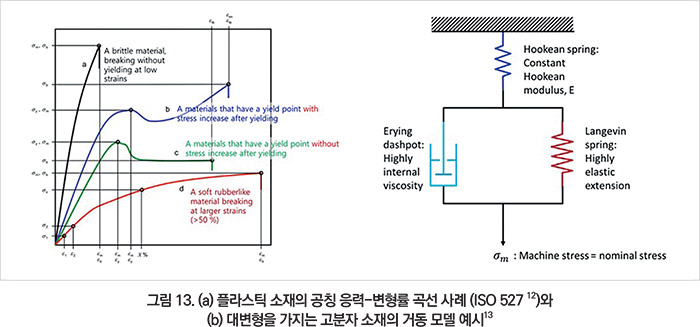
그림 14에 보여지는 바와 같이 탄성계수의 설정에 따라 소재의 탄-소성 거동이 확연하게 달라질 수 있으므로 신중하게 계산되어야 한다.
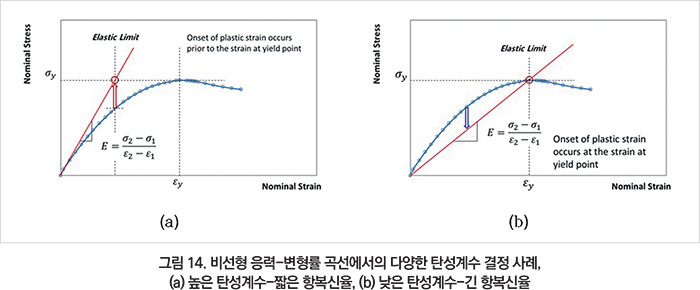
예를 들면, ISO 527의 제안에 따르면, 열가소성 플라스틱 소재의 탄성 계수(Tensile modulus, Et)는 e1=0.05%와 e2=0.25%와 사이의 변형 간격에서 응력-변형 곡선의 기울기로 계산한다. 일반적으로 ISO 527의 제안에 따라 탄성계수를 계산할 경우, 높은 탄성계수를 가지지만 항복신율이 짧아진다(그림 14a).
본 연구에서는 탄성 영역과 소성 영역을 구분하는 진응력 계산 방법인 식(10)과 영역 구분이 없는 전체 변형에 대한 진변형률 계산 방법인 식 (11)을 사용하여 공칭응력-공칭변형률 데이터로부터 진응력과 진변형률은 계산하였다.
대부분의 구조해석용 CAE 소프트웨어들이 탄성변형과 소성변형을 구분하여 사용한다. 탄성 변형률과 소성 변형률은 식 (12)와 식 (13)에 보여지는 바와 같이 전체 변형률에서 항복신율을 뺀 소성변형률을 계산할 수 있다.
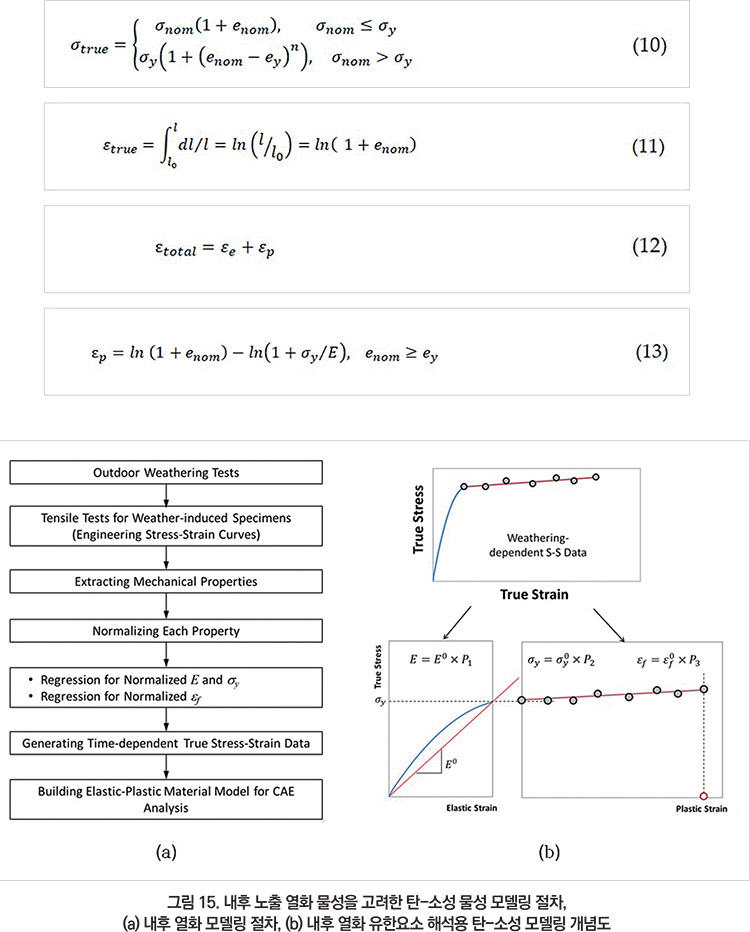
여기서 E은 탄성계수, σnom은 공칭 응력, enom은 공칭 변형률, σy은 항복강도, σtrue은 진응력, εtrue은 진변형률, n은 경화 지수이며, εtotal은 전체 진변형률, εe은 탄성 변형률, εp은 소성변형률이다.
자연광 노출 시간별 인장시험 결과로부터 유한요소 해석용 진응력-진변형률을 계산하는 절차는 그림 15에 정리한 바와 같다. 누적 광량에 대한 물성 유지율 개념을 도입하였으므로 탄성계수의 유지율(P1), 항복강도의 유지율(P2), 그리고 파단신율의 유지율(P3)을 각각 계산한다.
3.2. 내후 열화를 고려한 가상 부품 설계 사례
내후 열화를 고려한 부품 설계란 부품을 구성하는 소재가 누적 광량 또는 시간 경과에 따라 어떻게 반응하는지를 고려하는 소재의 열화 거동 모델링에서 출발한다. 내후 CAE 해석은 내후 노출시간이 지속되면서 발생하는 부품 성능을 예측하는 방식(Continuous time-dependent analysis)과 일정 시점이 지난 시점에서의 부품 성능을 예측하는 방식(Discontinuous time-dependent analysis)으로 구분할 수 있다(그림 16).
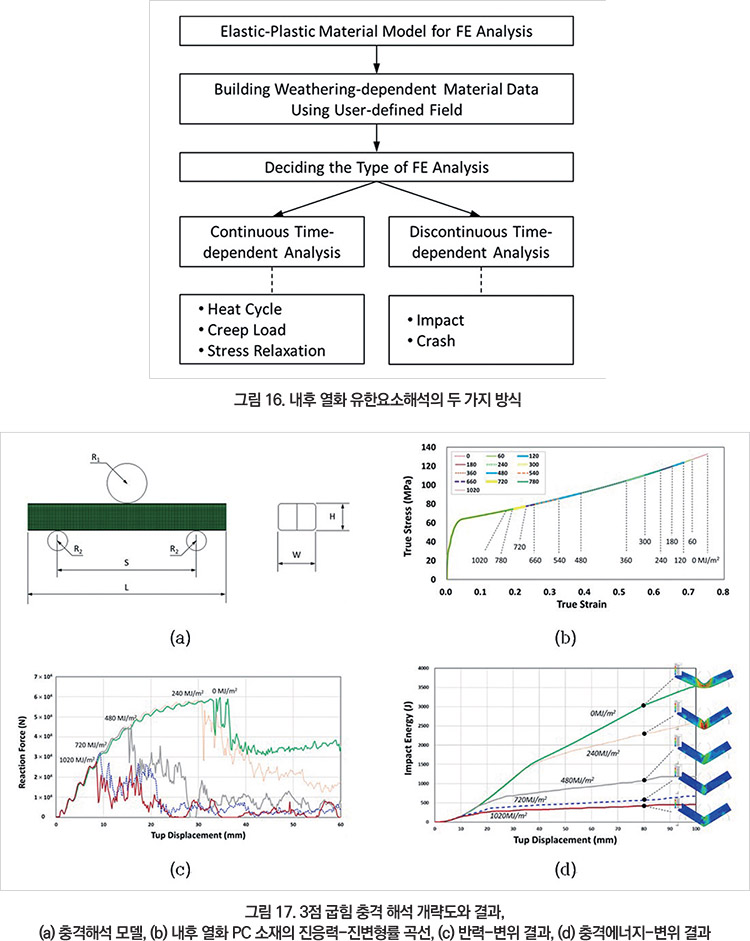
3.2.1. 불연속 내후 CAE 해석 사례 – PC 충돌 해석
자동차 범퍼의 충돌 부재에 대한 가상 사례로써, 그림 17a처럼 PC 소재로 된 이중 챔버 구조를 가진다(강체 충격 막대의 반경(R1) = 50㎜, 지지 막대 반경(R2) = 20㎜, 지점 거리(S) = 350㎜, 이중 챔버 채널 치수 = L×W×H = 500×90×70㎣). ABAQUS/Explicit를 사용하였으며, 유한요소 모델은 4 절점 쉘 요소(S4R)를 적용하였다.
강체 충돌 막대와 PC 챔버 사이의 마찰계수는 0.05로 설정하였고, PC 부품 자체는 0.15의 마찰계수로 자가 접촉(Self-contact)되는 것으로 설정하였다.
굽힘 충격 속도는 2m/s 설정하였다. PC 소재의 경우, 4년의 내후 노출기간 동안 탄성계수와 항복신율 변화는 무시할 만한 수준이었고, 파단신율의 저하만 관측되었다. 그림 15에 설명된 절차에 따라 내후 열화된 PC 소재의 진응력-진변형률 곡선을 생성하여 사용하였다(그림 17b).
그림 17c 및 17d에 보여지는 바와 같이 240MJ/㎡과 480MJ/㎡ 사이에서 반력 및 충격에너지가 급격하게 감소하는 것을 확인할 수 있다.
3.2.2. 연속 내후 CAE 해석 사례 (1) – PP 내후/내열 해석
균일 하중 70N을 지탱하며 자연광에 노출되는 플라스틱 하우징의 기온 변화 사이클에 대한 내후 CAE 해석을 수행하였다(그림 18). 사계절 기온 변화를 고려한 온도 사이클(그림 18b) PP 소재를 적용하였다.
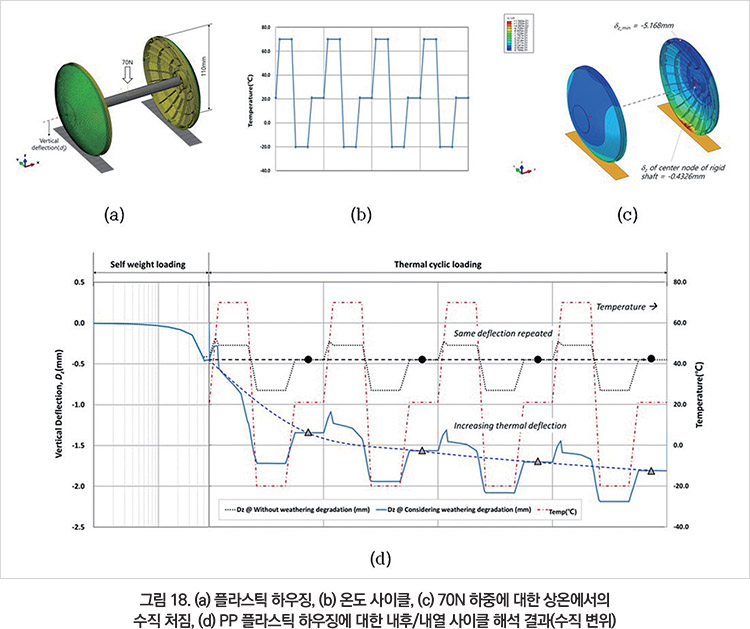
ABAQUS/Standard를 사용하였다. 균일 하중 70N에 의해 중심축이 약 0.43㎜ 이동하는 것으로 파악되었다(그림 18c). 균일 하중이 있는 크리프 조건에서 계절 변화에 의한 온도 사이클과 내후에 의한 물성 열화가 복합적으로 고려된다.
그림 18d에 보여지는 것처럼 크리프 변형과 내후 열화를 고려하지 않는다면 균일한 변형이 반복되는 비현실적 결과(검정색 점선)를 얻게 될 것이나, 물성 변화가 고려된다면 온도 사이클과 누적 광량이 증가할수록 처짐이 증가(청색 실선)하는 것을 알 수 있다.
3.2.3. 연속 내후 CAE 해석 사례 (2) – PBT 보스의 자기 풀림 해석
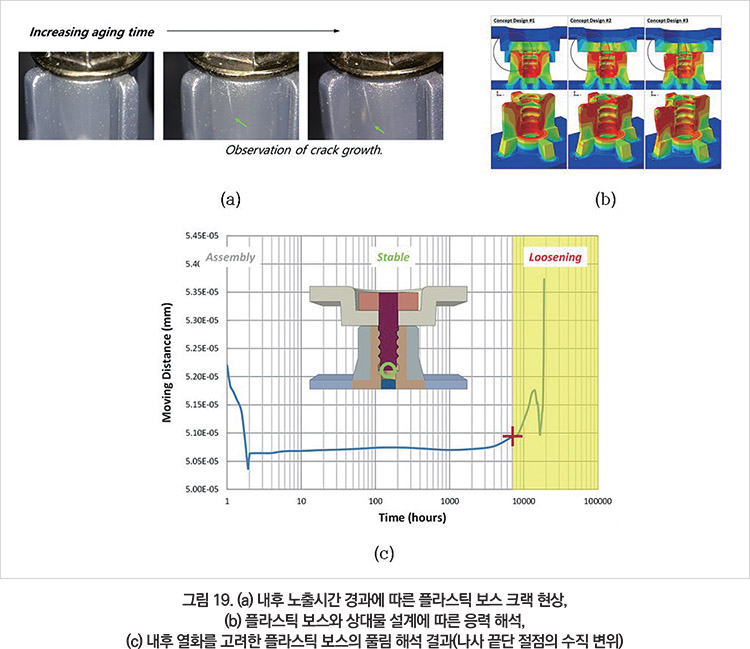
금속 나사가 조립된 플라스틱 보스가 내후 노출시간 경과함에 따라 나사 풀림(Screw loosening)이 발생하거나 크랙이 발생하고 성장하는 사례를 볼 수 있다(그림 19a). PBT 플라스틱 보스에 대해 다양한 보스 설계안에 대해 ABAQUS/Standard를 사용하여 플라스틱 보스의 응력 분포를 확인하였다(그림 19b).
나사 조립력을 받는 플라스틱 보스에 대해 내후 열화 물성을 고려하면, 나사 조립 후 조립력이 일정 시간 동안 유지되다가 내후 노출에 의한 물성 열화로 약해지기 시작하면서 나사의 이동이 발생하는 것을 예측할 수 있다(그림 19c).
Ⅲ. 맺음말
플라스틱 부품의 장기 수명 예측은 플라스틱 부품의 수명연장을 위한 기본 설계 자료를 제공할 수 있으므로, 탄소중립과 순환 경제 이슈가 더욱 강조되는 추세에서 재활용/재사용보다 더 적극적인 친환경 전략이 될 것이다.
■ 종래의 수많은 내후 선행연구에서 다루어지지 않았던 세 가지 내후 시험 인자(시편 거치 조건, 시편 두께, 잔류응력)에 대해 설명하였다.
■ 대표적인 내후 환경 노출 소재 4종(PC, PP, PBT, HDPE)에 대한 4년의 자연광 노출 시험 결과를 정리하여 제시하였고, 이를 활용한 두 가지 내후 수명 예측 모델(탄성 영역 물성 거동 예측을 위한 ‘지수 성장-감소 모델’과 소성 영역 물성 거동 예측을 위한 ‘역 로지스틱 모델’)을 제안하였다.
■ 내후 노출 플라스틱 부품의 수명연장을 위한 설계 방법으로 내후 CAE 해석 절차를 제안하였으며, 내후 열화를 고려한 두 가지 내후 CAE 해석 기법(내후 노출시간 경과 시점에서의 부품 성능을 예측하는 불연속 내후 CAE 해석과 지속적인 내후 시간 경과에 따른 부품의 성능 변화를 예측하는 연속 내후 CAE 해석)을 보여주었다.